Weiner Filter

The inverse filtering is a restoration technique for deconvolution, i.e., when the image is blurred by a known lowpass filter, it is possible to recover the image by inverse filtering or generalized inverse filtering. However, inverse filtering is very sensitive to additive noise. The approach of reducing one degradation at a time allows us to develop a restoration algorithm for each type of degradation and simply combine them. The Wiener filtering executes an optimal tradeoff between inverse filtering and noise smoothing. It removes the additive noise and inverts the blurring simultaneously.
The Wiener filtering is optimal in terms of the mean square error. In other words, it minimizes the overall mean square error in the process of inverse filtering and noise smoothing. The Wiener filtering is a linear estimation of the original image. The approach is based on a stochastic framework. The orthogonality principle implies that the Wiener filter in Fourier domain can be expressed as follows:
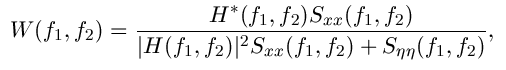
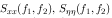where  are respectively power spectra of the original image and the additive noise, and  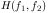is the blurring filter. It is easy to see that the Wiener filter has two separate part, an inverse filtering part and a noise smoothing part. It not only performs the deconvolution by inverse filtering (highpass filtering) but also removes the noise with a compression operation (lowpass filtering).

Weiner Filter note uploaded on my blog ajinkyaspeaks.wordpress.com for easy download!!
Just download it from the "Download box" present on ajinkyaspeaks.wordpress.com.

Kindly Bookmark and Share it: